1) رياضيات جوهر مفردهء عالم هستي است .
2) رياضيات زبان مشترك تمام آدمهاست .
3) رياضيات قاموس هستي را ورق مي زند .
4) رياضيات همان شاه كليد گشودن رازهاي هستي است .
5) رياضيات خالص شدهء تمامي علوم بشري است .
6) رياضيات ناموس هستي و يگانه بيان واقعيات جهان هستي است .
7) رياضيات جوهر و عصارهء همهء افكار وانديشه هاي بشري است .
8) رياضيات همان جان هستي بخش عالم ماده است .
9) رياضيات نيروي محركه و نظم دهندهء تفكرو انديشه است .
10) تمامي علوم در روند تكاملي به سوي رياضيات حركت مي كنند .
11) رياضيات همان مجموعه اشتراك تمامي علوم است .
12) رياضيات توجيه كنندهء ارتباط تمام ذرات كاينات است .
13) رياضيات پرده ها را بر مي دارد .
14) رياضيات پرده ها را يكي يكي بر مي دارد .
15) رياضيات جان كلام و روح هستي است .
16) رياضيات ستون عمارت فكر است .
17) رياضيات عشق مي آفريند .
18) رياضيات وحدت بخش تمامي پديده هاي هستي است .
19) رياضيات چيزي جز انسجام عقل نيست .
20) رياضيات موجب شادي روح است .
21) رياضيات خزانهء اسرار هستي است .
22) رياضيات روح واسكلت تفكرو بهترين وسيله براي منظم كردن انديشه هاست.
23) رياضيات تنها علم ازلي و ابدي است .
24) رياضيات به سخن و نوشته جان مي دهد .
25) رياضيات عشق و محبت مي آفريند .
26) رياضيات موجب سعادت است .
27) رياضيات قدرت به همراه دارد .
28) رياضيات رضايت آور است .
29) رياضيات منشاء زيباييهاست .
30) رياضيات همان تشعشعات مبداء فياض دركون و مكان است .
31) رياضيات قوهء محركهء هستي است .
32) رياضيات جان هستي است .
33) رياضيات كل غيرت كاينات است .
34) رياضيات ناموس و قاموس هستي است .
35) رياضيات هم درجوهرماده و هم درعرض آن،وجود مؤثر و نقش اساسي دارد .
36) بدون رياضيات قوام هستي بهم مي خورد .
37) تنها رياضيات مي تواند غايت ها را براي انسان آشكار سازد .
38) بدون رياضيات هيچ شييي ماهييت وجودي پيدا نخواهد كرد .
39) اگررياضيات رابردارند همة علوم ومعارف بسان حبابهاي صابون خواهندتركيد
40) ماهييت هر ذيوجودي با رياضيات عجين است .
41) هيچ پديده اي نمي تواند خارج از قلمرو رياضيات به وقوع بپيوندد .
42) تمامي زيباييها حكايت از حضور رياضيات مي كنند .
43) حقيقت چيزي جز قانونمنديهاي رياضي نيست .
44) اساس و ماهييت تفكر و انديشه رياضيات است .
45) رياضيات به انسان مدارا ، صبر و حوصله ميآموزد .
46) سيستم عامل درون مغز انسان مجموعه اي ازقوانين رياضيات است .
47) حتي مرگ و نيستي نيز قانو نمندي رياضي دارند .
48) درزشتي ها وزمختي ها نيزردپاي رياضيات ديده ميشود،به شرطي كه زيبانگرباشيم .
49) حقيقت زيباست و زيبايي حقيقت دارد ،و هردو جلوه هايي ازرياضيات هستند .
50) انفورماتيك فرزندخلف رياضيات است. انفورماتيك همان پردازش خودكار اطلاعات است.
51) انفورماتيك به كمك رياضيات بر جهان هستي استيلا يافت .
52) بدون انفورماتيك قوام زندگي بهم مي خورد .
53) بدون انفورماتيك انسان به دو هزار سال پيش برمي گردد.
54) اگر رياضيات سلطان علوم باشد، آنگاه سايبرنتيك همسر سلطان و انفورماتيك فرزند سلطان وكامپيوتر نوهء نازنازي سلطان علوم
خواهدبود.
55) كامپيوتر رياضيات نمي فهمد، ولي آنرا بسيار عالي بكار مي گيرد.
56) امروزه بيسواد كسي است كه از دانش سايبرنتيك مطلع نباشد، و آن بدون اطلاعات رياضي ميسرنخواهد بود . لذا بيسواد
اصلي كسي است كه از رياضي بي بهره باشد .
57) معلمان رياضي افتخار مضاعف نصيبشان شده است ،زيرا در شاهراه بزرگترين رسالت بشر يعني ،، معلمي ،، از بهترين
وسيلهء حركت براي پيمودن مسير يعني ،، رياضيات ،، استفاده مي كنند .
58) تدريس يك هنراست اما تدريس رياضيات هنري برتر،يعني هنر علمي است .
59) زاحمدتااحديك ميم فرق است معلم را نگر در ميم غرق است .
60) معلم را فكر و عزم راسخ است همه حال اوبرسش وباسخ است.
61) مطالعه مستمر و دايم براي معلم همچون نفس كشيدن است.
62) معلم آيينه ايست كه دانش آموزان آيندهء خود را در او مي بينند .
63) مسير معلمي مسير عشق است .
64) معلم عاشقي است كه در مسير عشق، عشق را با عشق معني ميكند .
65) معلم واقعي براي همه دل مي سوزاند،اگرچه حتي يك نفر هم براي او دل نسوزاند .
66) شجاعا نند كه مسيرهاي خطرناك را انتخاب مي كنند . لذا معلمين شجاعترين شجاعا نند.
67) مسير معلمي خطرناكترين مسيري است كه انسان در پيش مي گيرد، چرا كه درآنجا بايد با ديوجهالت نبردي وحشتناك
داشته باشد .
68) اگر حباب همه چشم است ، معلم همه شور است .
69) مهم مثل معلم غرق در ميم است ، از هر طرف برخواني مهم دارد نشاني .
70) به زعم بعضيها ، معلم اول و آخرش ميم است ، لذا اول مانده و آخر ماندة زندگيست ! اما به زعم من ، معلم اول
مست وآخرنيز مست است از مي الست .
71) كلاس آرامگاه معلم است .
72) تمامي متفكران عالم در چاه تناقض دست و پا مي زنند و سرگردانند .آ نچه هست وحدت وجود است در كثرت نمود .
73) ماديات پايگاهي است براي پرتاب موشك معنويات .
74) خوشبختي چيزي جز رضايت درون انسان نيست .
75) خوشبخت هيچگاه منتظراظهارنظرديگران درمورد اوضاع و احوال خود نيست .
76) سعادت تو در آن است كه به انتخابي دست بزني كه هيچگاه ازآن عمل پشيمان نشوي.
77) كسي كه به ارزشهاي اعتباري ديگران دل خوش كند،هرگزبه سعادت نخواهد رسيد .
78) سعادتمند كسي است كه درونش همواره شاد باشد،و هيچ موردي نتواند شادي اورا تحت تاثيرقرار دهد. حتي شنيدن اين
خبر كه : ،، شادي فقط يك فرض دروني است و اصلاً وجود خارجي ندارد ! ،،
79) خود را خوشبخت دانستن فقط يك احساس دروني است ، اما سعادت داشتن چيزي ماوراي احساس بوده و بعضيها سعادت
خود را در نمي يابند .
80) اگر انسان از طبيعت خود دور نمي شد، به همهء آرزوهايش مي رسيد .
81) اگرانسان تكليفش راباخودش روشن كند،تكليف اوباديگران كاملاًروشن است .
82) اگرانسان بتوا ند با خودش كناربيايد ،به راحتي با ديگران نيزكنارخواهد آمد .
83) كسي كه مدام باديگران سرجنگ دارد،در واقع باخودش مي جنگدو درونش آشوب است.
84) اگر زيبا بنگريم ، زشت ها نيز زيبا هستند .
85) نيازمند فقط كسي است كه معرفت و عقل كم دارد .
86) اگر راهنما چند تا شو ند ، چاه نما مي شوند .
87) گاهي راه بيفته جا ميفته ، گاهي جا بيفته راه ميفته !
88) وحشتناكترين لحظات براي انسان دانا زماني است كه براي سؤالش پاسخي نباشد.
89) تلخي اگر از حد بگذرد شيرين شود !
90) مسكرترين مسكر براي يك انسان جهل و ناداني است .
91) انسان چيزي جز حاصل انتخابهايش نيست .
92) سازگاري آري ولي سازشكاري نه .
93) دلبستگي هرگز، وابستگي چرا،پيوستگي گاهي .
94) هنر راهي است بسوي زيبايي ، اما چون پر رهرو است سهم زيبايي كمتر مي شود . علم نيز راهي است بسوي زيبايي ،
وليكن با رهرواني معدود و تصاحب اكثرزيباييها !
95) ديوار هنر بسياركوتاه ، ولي ديوار علم بسيار بلند است .
96) هر عالمي مي تواند هنرمند گردد ، اما هر هنرمندي عالم نتواند شد .
97) هنرمندي، ويژگي عام ولي عالم شدن حالتي خاص ، وهردو مي توانند مرزها را بشكنند .
98) انسان برخود مسلط،مي توانددرهرجايي پناهگاهي براي تجسم كردن بيابد .
99) دوستي همراه با دورشدن ازهويت خود،عين دشمني،ودشمني توام با به رسميت شناختن استقلال فردي عين دوستي است.
100) نثر بستر خواب كلمات است ، و شعر ميدان ورزش براي واژه ها .
101) پايبندي به اصول آرماني موجب عزت و احترام و منزلت است .
102) اول فكر كردن و بعد سخن گفتن شيوهء دانايان است .
103) همهء رنجها ناشي از سرعت فكر كردن است . چنانچه
سرعتش به حداقل كاهش يابد آرامش فرا مي رسد . البته فكر كردن هرگز متوقف
نخواهد شد .
104) توقف و سكون حتي دروقت عدم فهم نيز جايزنيست، بايستي حركت كرد ، خود مسير راهنماي چگو نه طي كردن آن بوده و بارقه هاي فهم و درك در پي ما خواهند آمد .
105) در قضاوت كردن هرچه بيشتر تاخير كنيم ، شايد به
آنچه كه هست تا حدودي نزديك شويم . نبايد غافل بود كه رسيدن به آنچه كه
هست محال است .
106) هر چند به راه خود اطمينان داشته باشيم ، اما واپس نگريستن و ارزيابي مسير ، نشان ازجامعيت معرفت و شناخت ماست .
107) نوشته ها بيشتر از بيان ، سطح معرفت صاحب قلم را بر ملا مي كنند .







 نتیجه می شود
نتیجه می شود



 نتیجه می شود
نتیجه می شود
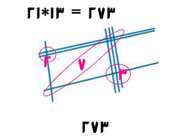
 خاصیت جالبی دارد. از رابطه ی
خاصیت جالبی دارد. از رابطه ی  نتیجه می شود ،
نتیجه می شود ،
 ، عدد
، عدد  عددی است ۹ رقمی که همه ی ارقامش مساوی k است . اینک
عددی است ۹ رقمی که همه ی ارقامش مساوی k است . اینک را اختیار می کنیم . از رابطه ی
را اختیار می کنیم . از رابطه ی 































 $$$$$$$_________$$$$$$$
$$$$$$$_________$$$$$$$